Contributed by:
Maths Jan 2019 IGCSE Math Sheet their Numbers, algebra, statistics, and geometry Questions available
2.
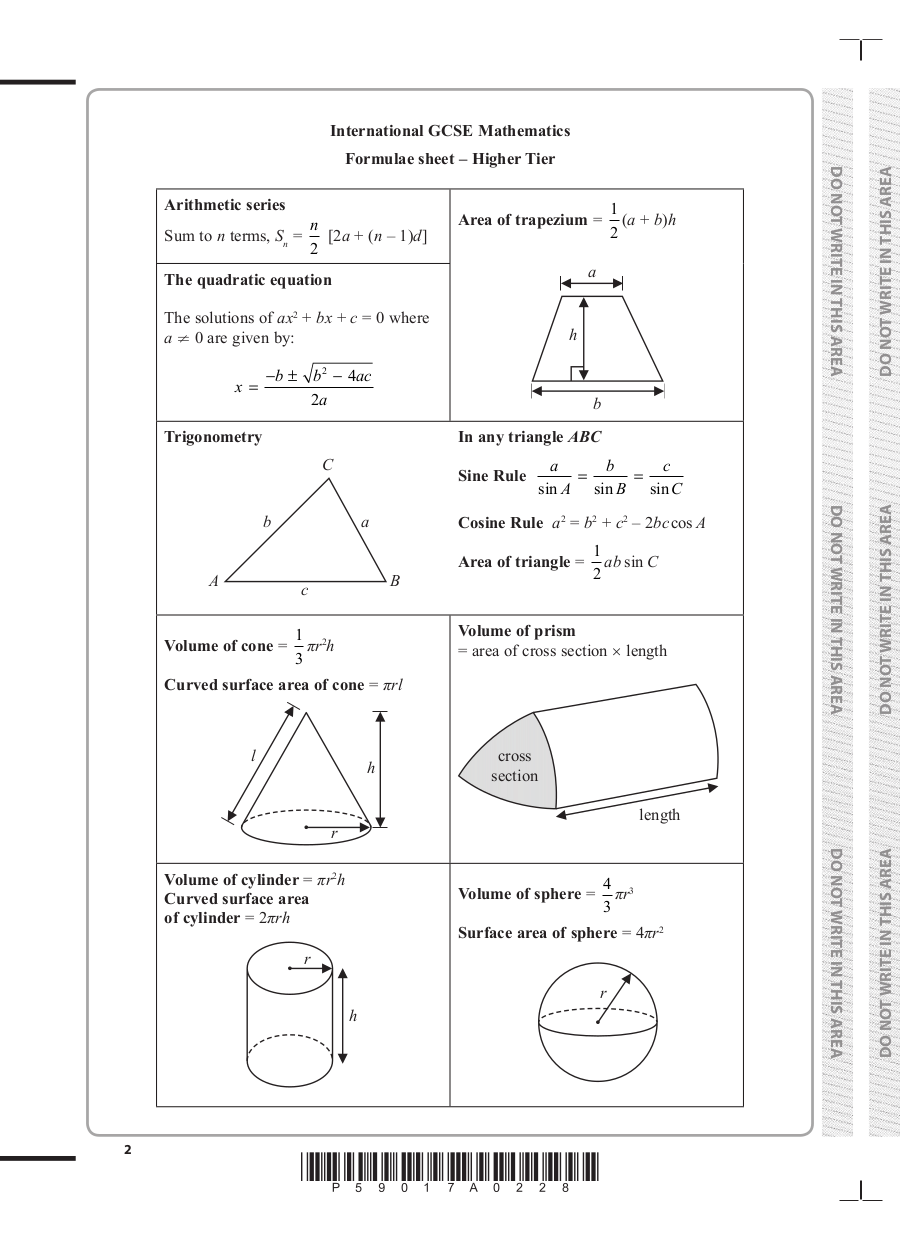
International GCSE Mathematics
Formulae sheet – Higher Tier
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
Arithmetic series 1
n Area of trapezium = (a + b)h
Sum to n terms, Sn = [2a + (n – 1)d] 2
2
The quadratic equation a
The solutions of ax2 + bx + c = 0 where
a ¹ 0 are given by: h
−b ± b2 − 4ac
x=
2a b
Trigonometry In any triangle ABC
C a b c
Sine Rule = =
sin A sin B sin C
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
b a Cosine Rule a2 = b2 + c2 – 2bccos A
1
Area of triangle = ab sin C
A B 2
c
1 2 Volume of prism
Volume of cone = πr h = area of cross section × length
3
Curved surface area of cone = πrl
l cross
h section
length
r DO NOT WRITE IN THIS AREA
Volume of cylinder = πr2h 4 3 DO NOT WRITE IN THIS AREA
Curved surface area Volume of sphere = πr
3
of cylinder = 2πrh
Surface area of sphere = 4πr2
r
r
h
*P59017A0228*
3.
Answer ALL TWENTY ONE questions.
Write your answers in the spaces provided.
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
You must write down all the stages in your working.
1 (a) Factorise fully 4p + 6pq
(2)
(b) Expand and simplify (e + 3)(e – 5)
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
(2)
2y + 1
(c) Solve y =
5
Show clear algebraic working.
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
y=
(3)
(Total for Question 1 is 7 marks)
3
*P59017A0328* Turn over
4.
y
10
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
A
8
6
B
4
2
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
–4 –2 O 2 4 6 8 x
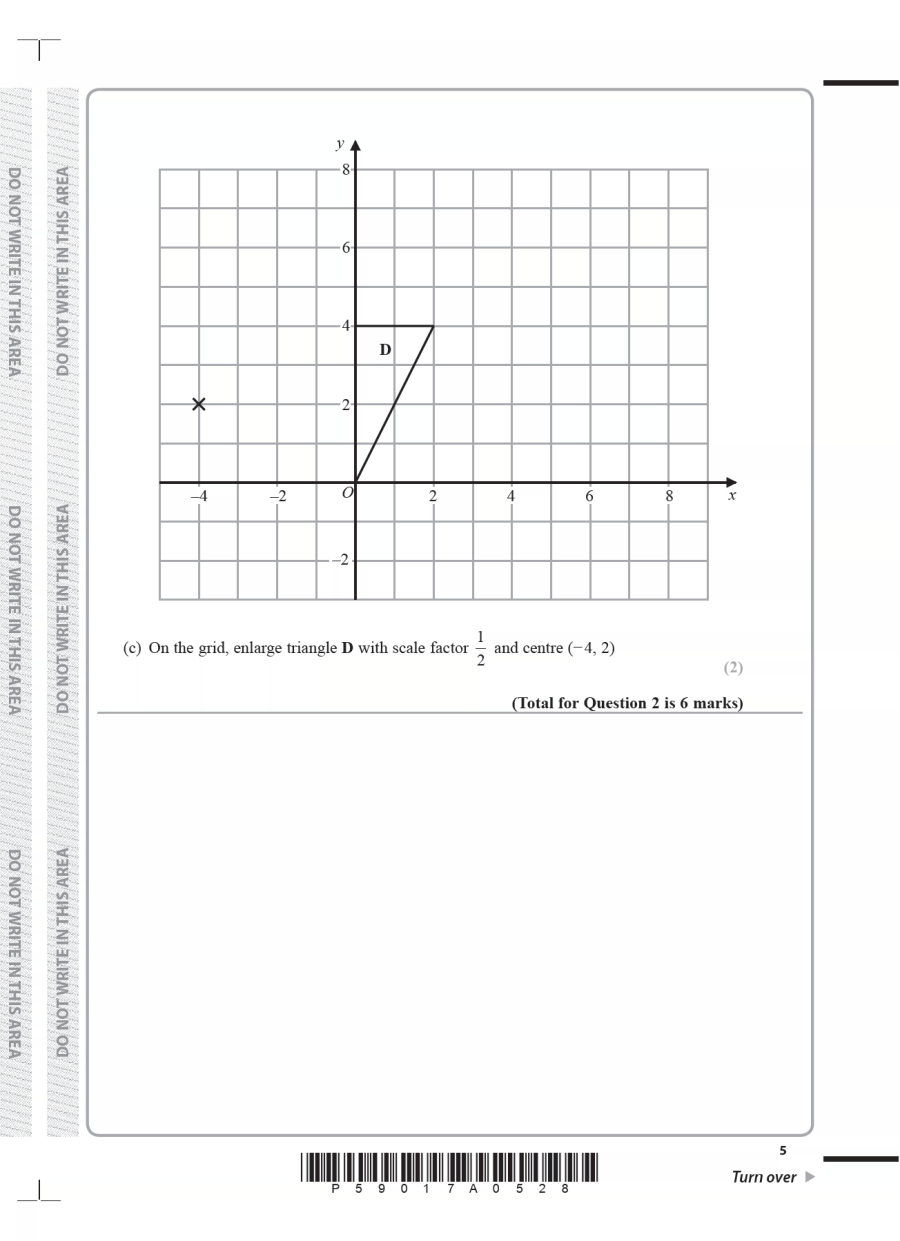
(a) Describe fully the single transformation that maps triangle A onto triangle B.
(3)
2
(b) On the grid, translate triangle A by the vector
−5
Label the new triangle C.
(1)
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
4
*P59017A0428*
7.
4 The table gives information about the price of gold.
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
1st February 2016 1st March 2016
Price of one ounce of
1126.50 1236.50
gold (dollars)
(a) Work out the percentage increase in the price of gold between 1st February 2016 and
1st March 2016
Give your answer correct to 3 significant figures.
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
%
(3)
The price of one ounce of gold on 1st February 2016 was 1126.50 dollars.
The price of gold increased by 19% from 1st February 2016 to 1st July 2016
(b) Work out the price of one ounce of gold on 1st July 2016
Give your answer correct to the nearest dollar.
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
dollars
(3)
(Total for Question 4 is 6 marks)
7
*P59017A0728* Turn over
8.
D
Diagram NOT
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
C
(30x – 5)° accurately drawn
(4x + 15)°
B
E
(20x + 45)°
F
A
BCD and AFE are straight lines.
Show that BCD is parallel to AFE.
Give reasons for your working.
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
(Total for Question 5 is 5 marks)
8
*P59017A0828*
9.
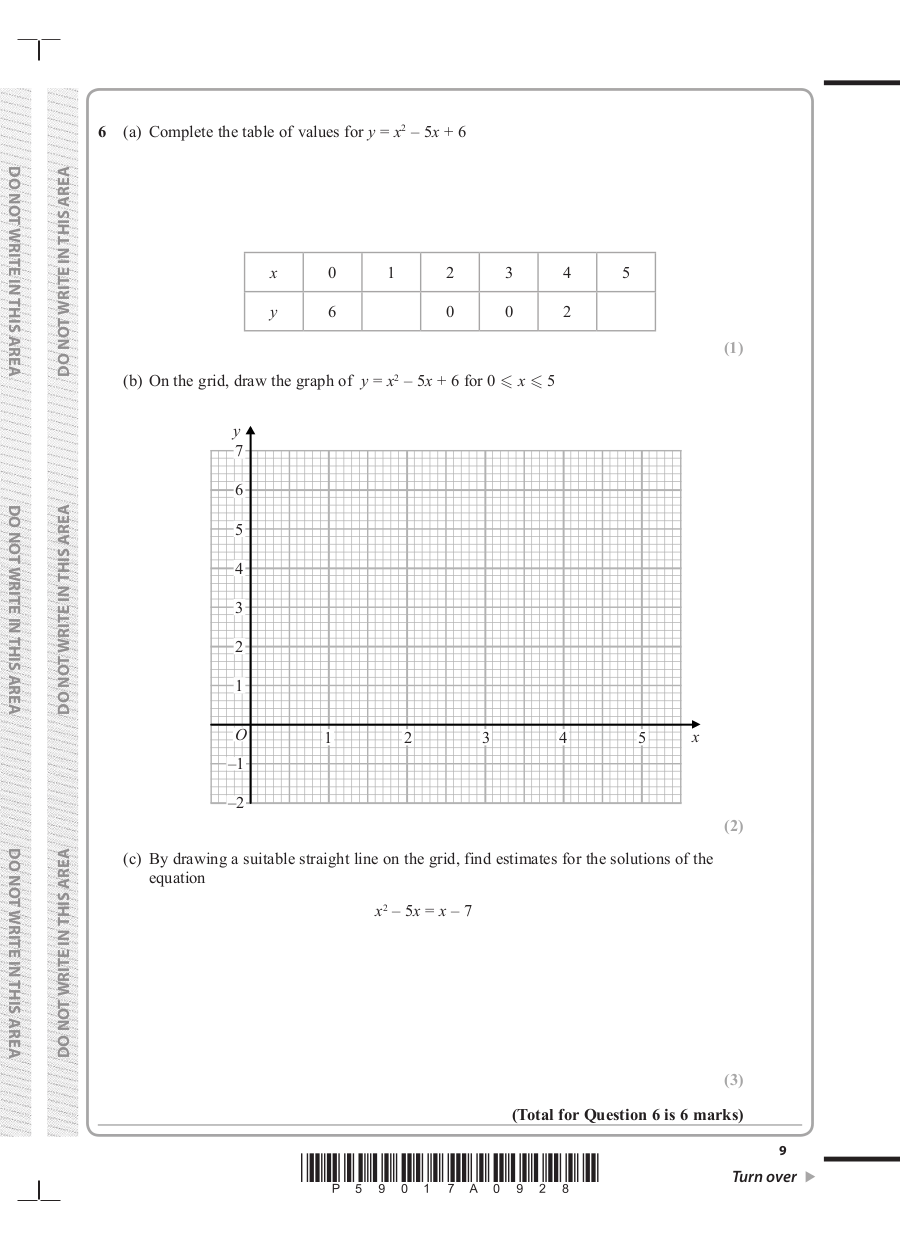
6 (a) Complete the table of values for y = x2 – 5x + 6
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
x 0 1 2 3 4 5
y 6 0 0 2
(1)
(b) On the grid, draw the graph of y = x2 – 5x + 6 for 0 x 5
y
7
6
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
5
4
3
2
1
O 1 2 3 4 5 x
–1
–2
(2)
(c) By drawing a suitable straight line on the grid, find estimates for the solutions of the
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
equation
x2 – 5x = x – 7
(3)
(Total for Question 6 is 6 marks)
9
*P59017A0928* Turn over
10.
7 The table shows the volumes, in km3, of four oceans.
Ocean Volume (km3)
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
Arctic Ocean 1.88 ´ 107
Atlantic Ocean 3.10 ´ 108
Indian Ocean 2.64 ´ 108
Southern Ocean 7.18 ´ 107
(a) Write 7.18 ´ 107 as an ordinary number.
(1)
(b) Calculate the total volume of these four oceans.
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
km3
(2)
The volume of the South China Sea is 9 880 000 km3
(c) Write 9 880 000 in standard form.
(1)
(Total for Question 7 is 4 marks) DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
10
*P59017A01028*
11.
8 The diagram shows an isosceles triangle.
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
Diagram NOT
accurately drawn
x cm x cm
5 cm
The area of the triangle is 12 cm2
Work out the perimeter of the triangle.
Give your answer correct to 3 significant figures.
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
cm
(Total for Question 8 is 4 marks)
11
*P59017A01128* Turn over
12.
9 The table shows information about the speeds of 60 cycles.
Speed (s km/h) Frequency
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
0 < s 10 3
10 < s 20 16
20 < s 30 24
30 < s 40 10
40 < s 50 5
50 < s 60 2
(a) Complete the cumulative frequency table.
Cumulative
Speed (s km/h)
frequency
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
0 < s 10
0 < s 20
0 < s 30
0 < s 40
0 < s 50
0 < s 60
(1)
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
12
*P59017A01228*
13.
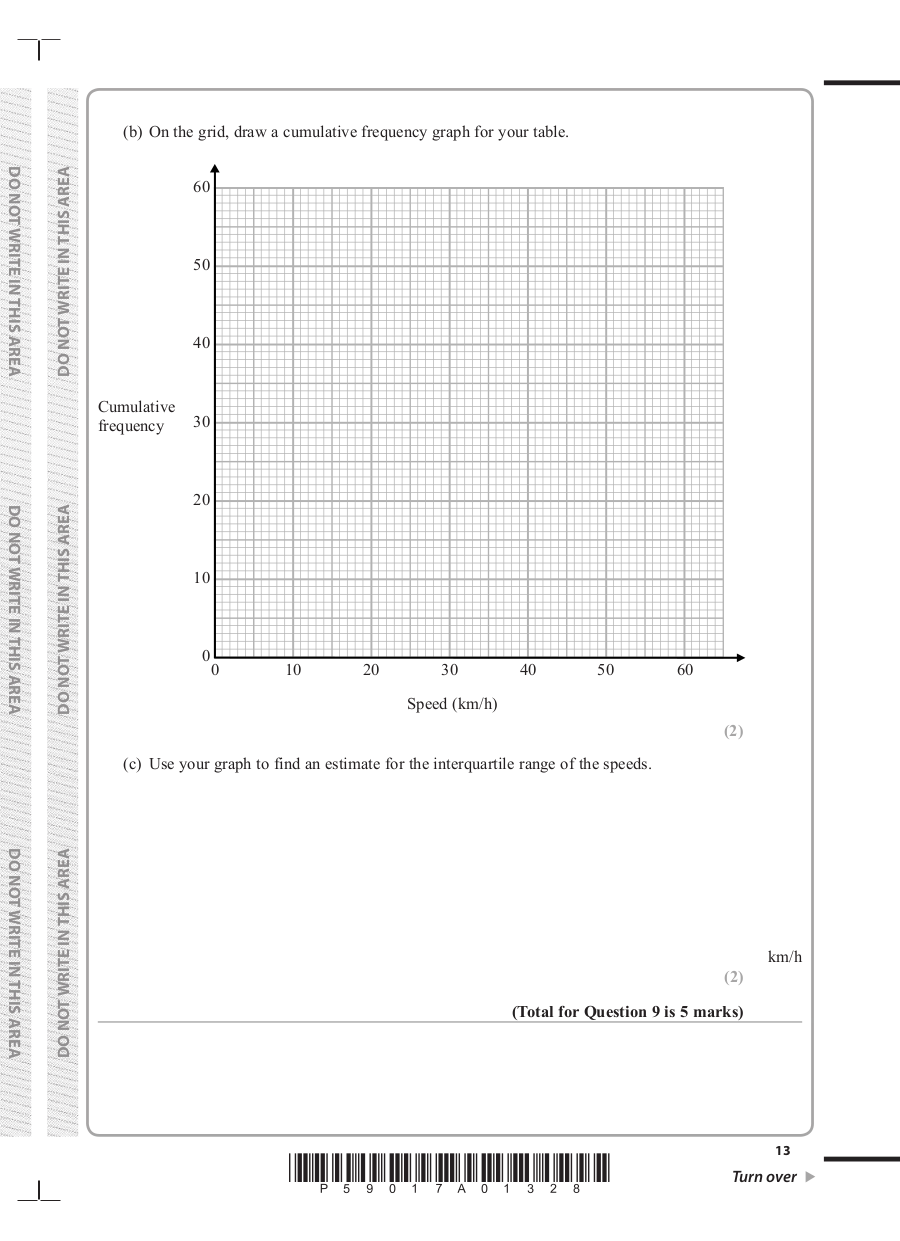
(b) On the grid, draw a cumulative frequency graph for your table.
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
60
50
40
Cumulative
frequency 30
20
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
10
0
0 10 20 30 40 50 60
Speed (km/h)
(2)
(c) Use your graph to find an estimate for the interquartile range of the speeds.
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
km/h
(2)
(Total for Question 9 is 5 marks)
13
*P59017A01328* Turn over
14.
10 Here is triangle ABD.
B
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
Diagram NOT
8 cm accurately drawn
C
20°
A D
13 cm
The point C lies on BD.
AD = 13 cm BC = 8 cm angle ADB = 90° angle CAD = 20°
Calculate the size of angle BAC.
Give your answer correct to 1 decimal place.
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
°
(Total for Question 10 is 5 marks)
14
*P59017A01428*
15.
5 x+2
11 Express − as a single fraction in its simplest terms.
3 2x
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
(Total for Question 11 is 3 marks)
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
15
*P59017A01528* Turn over
16.
1
12 The curve C has equation y = x3 − 9 x + 1
3
dy
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
(a) Find
dx
dy
=
dx
(2)
(b) Find the range of values of x for which C has a negative gradient.
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
(3)
(Total for Question 12 is 5 marks)
16
*P59017A01628*
17.
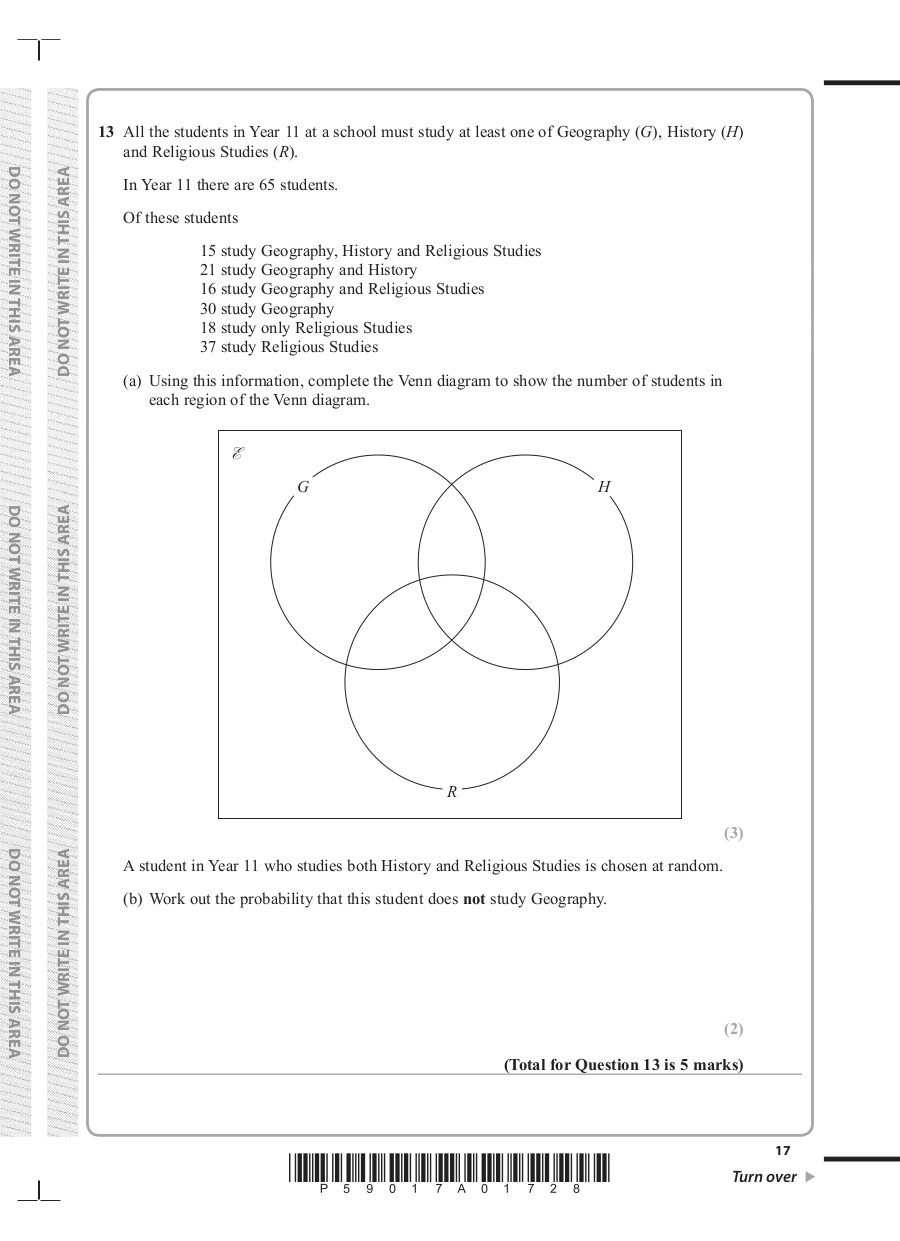
13 All the students in Year 11 at a school must study at least one of Geography (G), History (H)
and Religious Studies (R).
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
In Year 11 there are 65 students.
Of these students
15 study Geography, History and Religious Studies
21 study Geography and History
16 study Geography and Religious Studies
30 study Geography
18 study only Religious Studies
37 study Religious Studies
(a) Using this information, complete the Venn diagram to show the number of students in
each region of the Venn diagram.
E
G H
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
R
(3)
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
A student in Year 11 who studies both History and Religious Studies is chosen at random.
(b) Work out the probability that this student does not study Geography.
(2)
(Total for Question 13 is 5 marks)
17
*P59017A01728* Turn over
18.
14 T is directly proportional to the cube of r
T = 21.76 when r = 4
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
(a) Find a formula for T in terms of r
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
(3)
(b) Work out the value of T when r = 6
(1)
(Total for Question 14 is 4 marks)
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
18
*P59017A01828*
19.
15 The total surface area of a solid hemisphere is equal to the curved surface area of a cylinder.
The radius of the hemisphere is r cm.
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
The radius of the cylinder is twice the radius of the hemisphere.
Given that
volume of hemisphere : volume of cylinder = 1 : m
find the value of m.
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
m=
(Total for Question 15 is 4 marks)
19
*P59017A01928* Turn over
20.
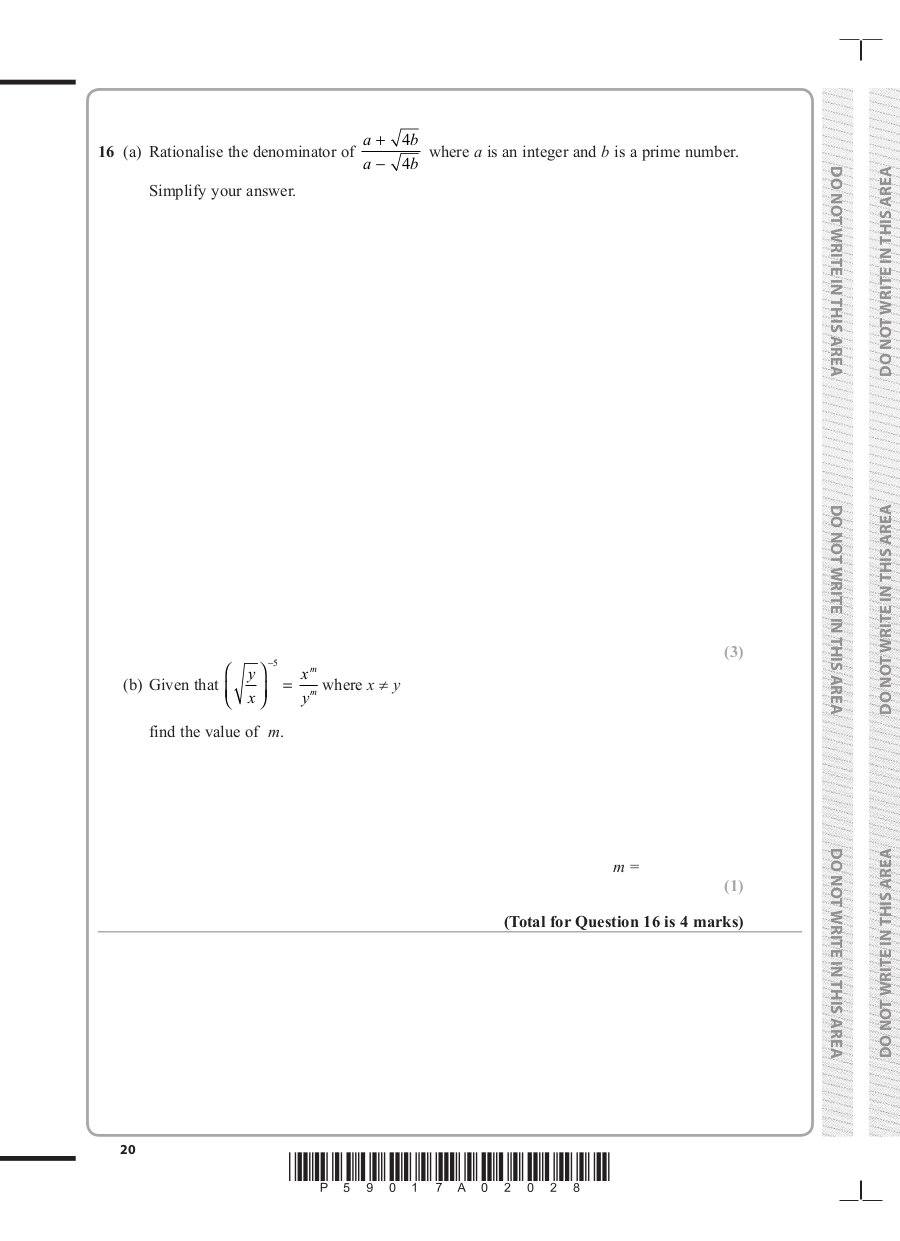
a + 4b
16 (a) Rationalise the denominator of where a is an integer and b is a prime number.
a − 4b
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
Simplify your answer.
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
(3)
−5
y xm
(b) Given that = where x ≠ y
x ym
find the value of m.
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
m=
(1)
(Total for Question 16 is 4 marks)
20
*P59017A02028*
21.
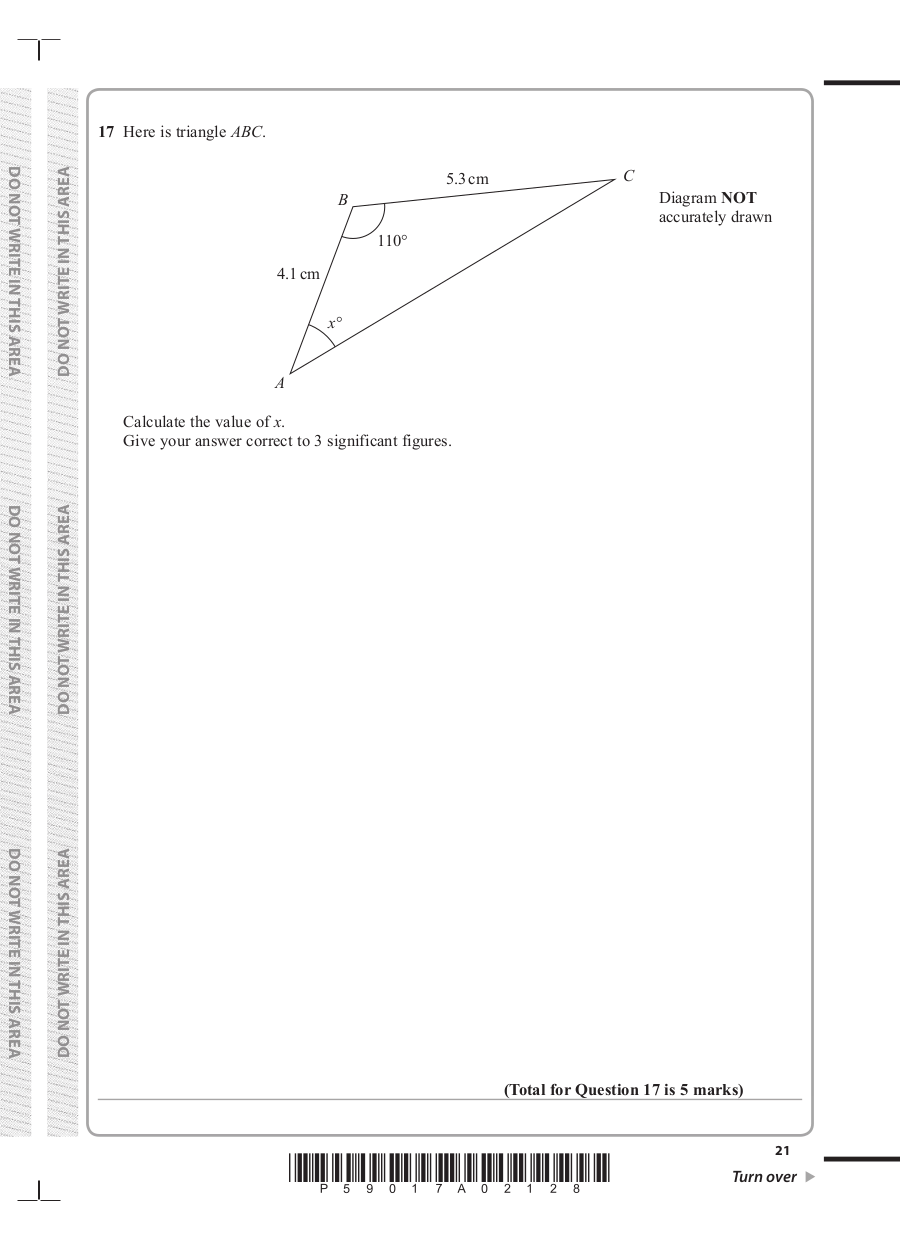
17 Here is triangle ABC.
C
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
5.3 cm
B Diagram NOT
accurately drawn
110°
4.1 cm
x°
A
Calculate the value of x.
Give your answer correct to 3 significant figures.
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
(Total for Question 17 is 5 marks)
21
*P59017A02128* Turn over
22.
18 The graph of y = f(x) is shown on the grid.
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
y
4
2
−8 −6 −4 −2 O 2 4 6 8 x
−2
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
−4
−6
−8
1
(a) On the grid above, sketch the graph of y = f x
2
(2)
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
22
*P59017A02228*
23.
The graph of y = f(x + k) is shown on the grid below.
y
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
4
2
−8 −6 −4 −2 O 2 4 6 8 x
−2
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
−4
−6
−8
(b) Write down the value of k
(1)
(Total for Question 18 is 3 marks)
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
23
*P59017A02328* Turn over
24.
19 g is the function with domain x –3 such that g(x) = x2 + 6x
(a) Write down the range of g–1
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
(1)
(b) Express the inverse function g–1 in the form g–1 : x
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
g–1 : x
(4)
(Total for Question 19 is 5 marks)
24
*P59017A02428*
25.
20 A bowl contains n pieces of fruit.
Of these, 4 are oranges and the rest are apples.
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
Two pieces of fruit are going to be taken at random from the bowl.
1
The probability that the bowl will then contain (n – 6) apples is
3
Work out the value of n
Show your working clearly.
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
(Total for Question 20 is 6 marks)
25
*P59017A02528* Turn over
26.
21 (2x + 23), (8x + 2) and (20x – 52) are three consecutive terms of an arithmetic sequence.
Prove that the common difference of the sequence is 12
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA
(Total for Question 21 is 4 marks)
TOTAL FOR PAPER IS 100 MARKS
26
*P59017A02628*
27.
27
*P59017A02728*
BLANK PAGE
DO NOT WRITE IN THIS AREA DO NOT WRITE IN THIS AREA DO NOT WRITE IN THIS AREA
DO NOT WRITE IN THIS AREA DO NOT WRITE IN THIS AREA DO NOT WRITE IN THIS AREA
28.
DO NOT WRITE IN THIS AREA DO NOT WRITE IN THIS AREA DO NOT WRITE IN THIS AREA
*P59017A02828*
BLANK PAGE
28