Contributed by:
Two triangles are said to be congruent if all three corresponding sides are equal and all three corresponding angles are equal in measure.
1.
Name:
Exam Style Questions
Ensure you have: Pencil, pen, ruler, protractor, pair of compasses and eraser
You may use tracing paper if needed
1. Read each question carefully before you begin answering it.
2. Don’t spend too long on one question.
3. Attempt every question.
4. Check your answers seem right.
5. Always show your workings
Revision for this topic
2.
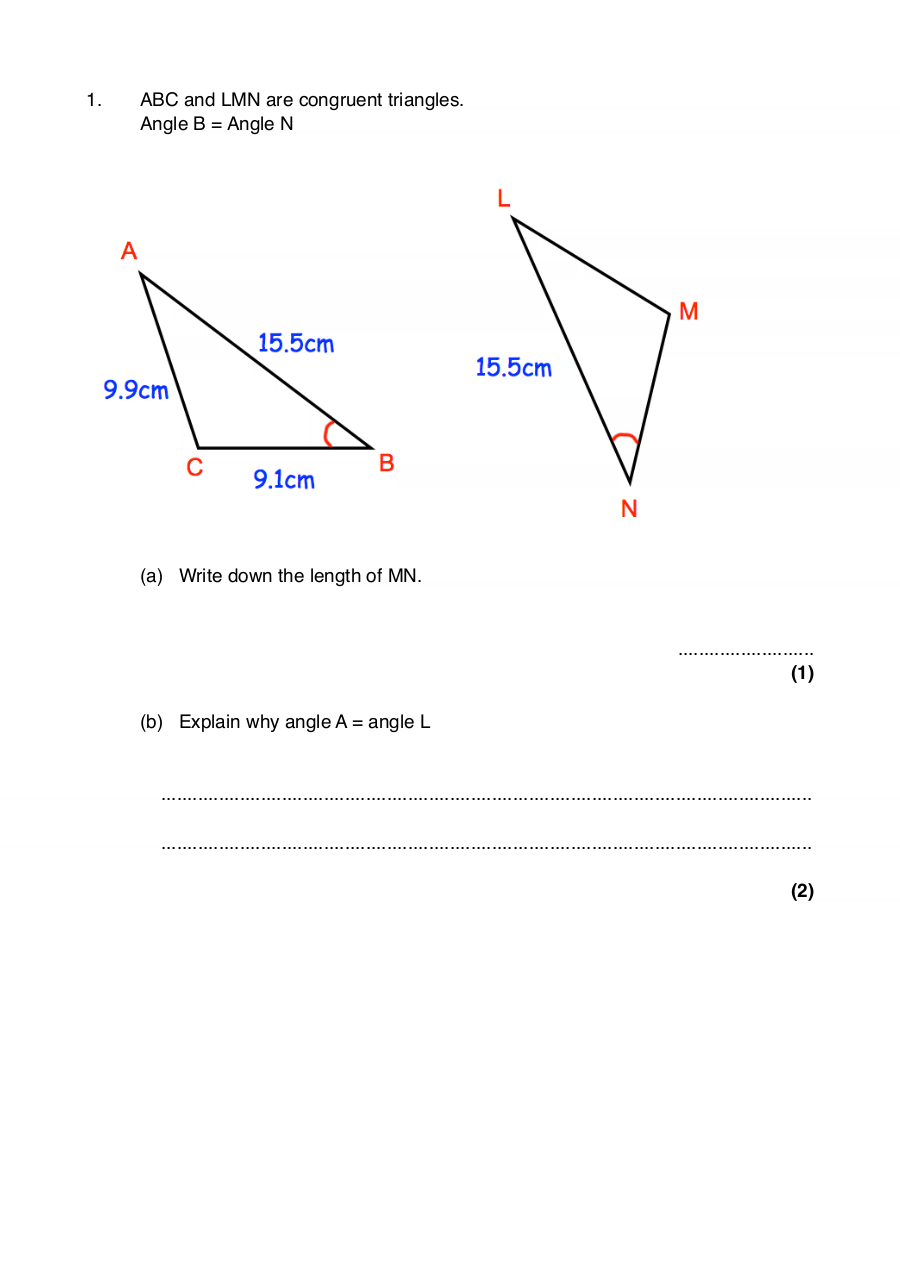
1. ABC and LMN are congruent triangles.
Angle B = Angle N
(a) Write down the length of MN.
..........................
(1)
(b) Explain why angle A = angle L
............................................................................................................................
............................................................................................................................
(2)
3.
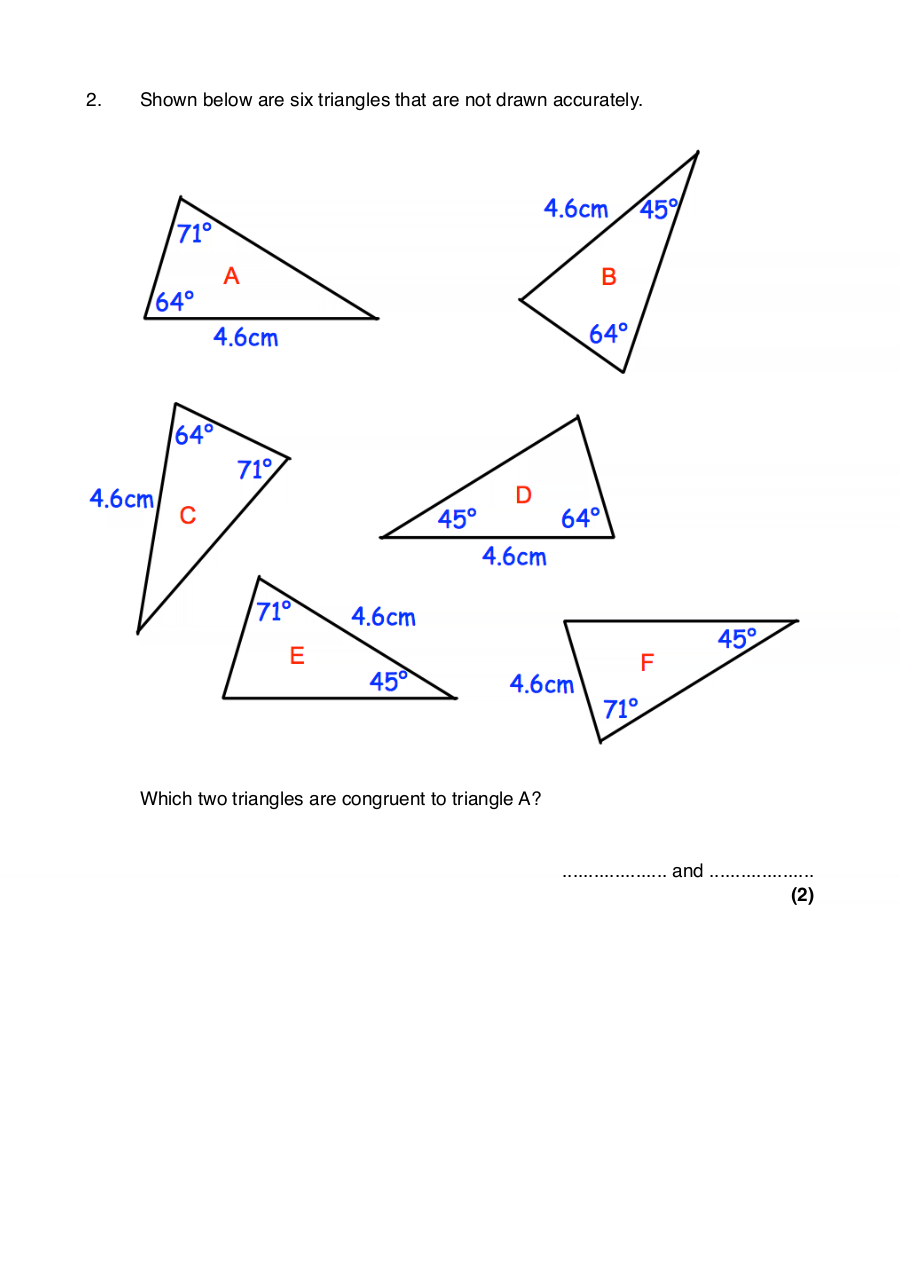
2. Shown below are six triangles that are not drawn accurately.
Which two triangles are congruent to triangle A?
.................... and ....................
(2)
4.
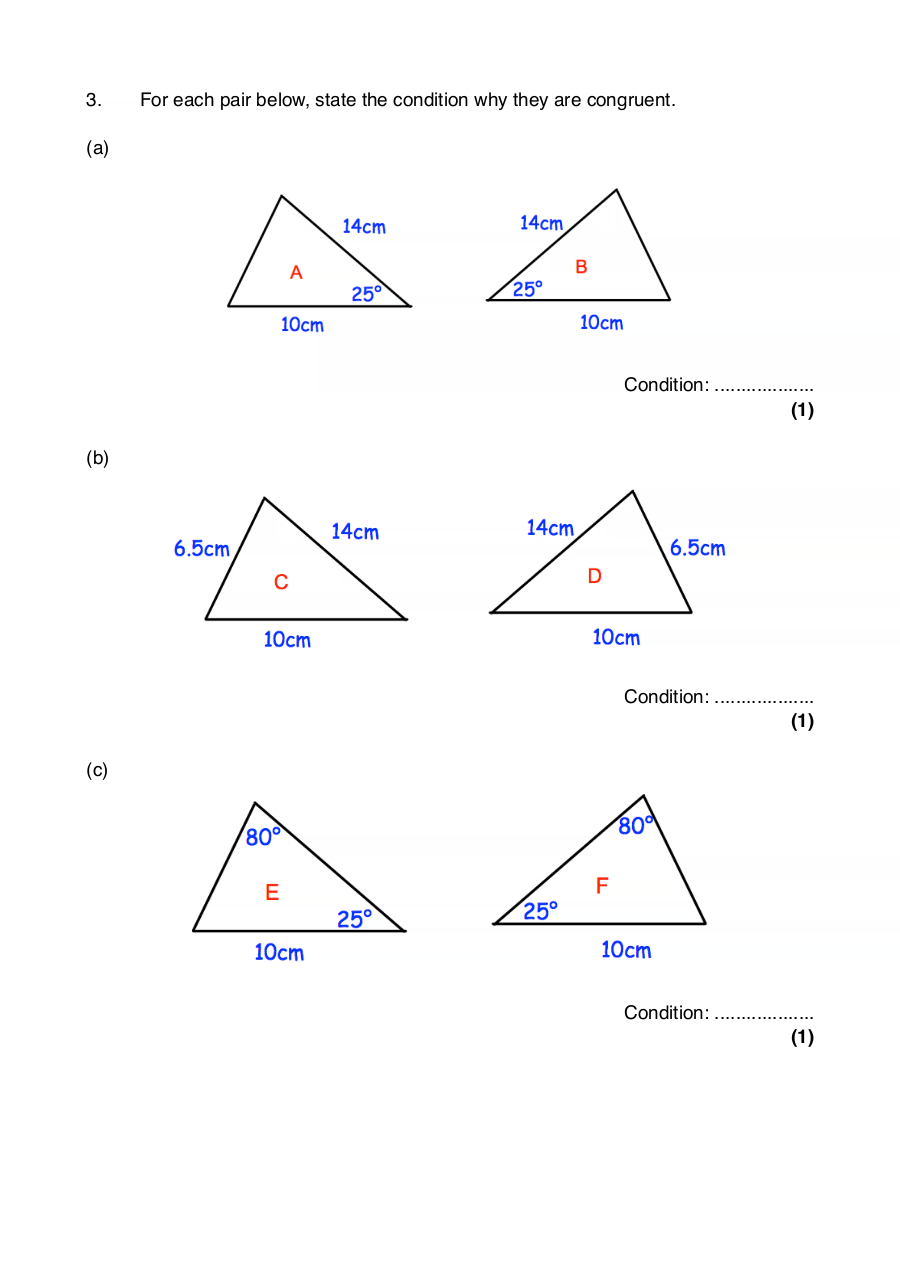
3. For each pair below, state the condition why they are congruent.
Condition: ...................
(1)
Condition: ...................
(1)
Condition: ...................
(1)
5.
4. James and Chris each draw a triangle with one side of 10cm, one angle of 45°
and one angle of 85°.
James says their triangles are congruent.
Explain why James is incorrect.
............................................................................................................................
............................................................................................................................
............................................................................................................................
(2)
5. ABCD is a parallelogram.
Prove that triangles ABD and BCD are congruent.
(4)
6. Two of the triangles below are congruent.
6.
Identify the two congruent triangles and explain your answer.
.................. and ....................
Reason: ............................................................................................................................
............................................................................................................................
............................................................................................................................
............................................................................................................................
............................................................................................................................
............................................................................................................................
(4)
7.
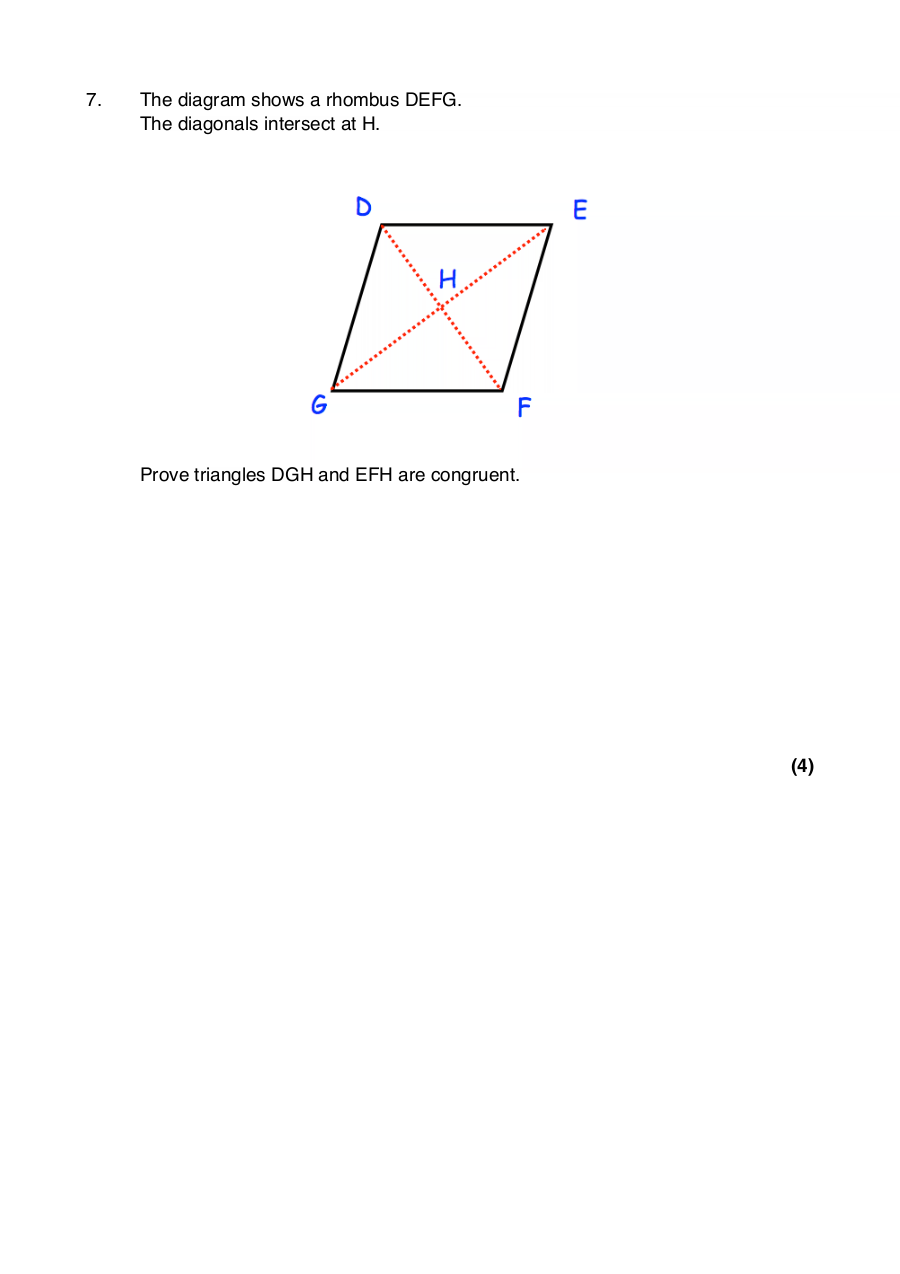
7. The diagram shows a rhombus DEFG.
The diagonals intersect at H.
Prove triangles DGH and EFH are congruent.
(4)
8.
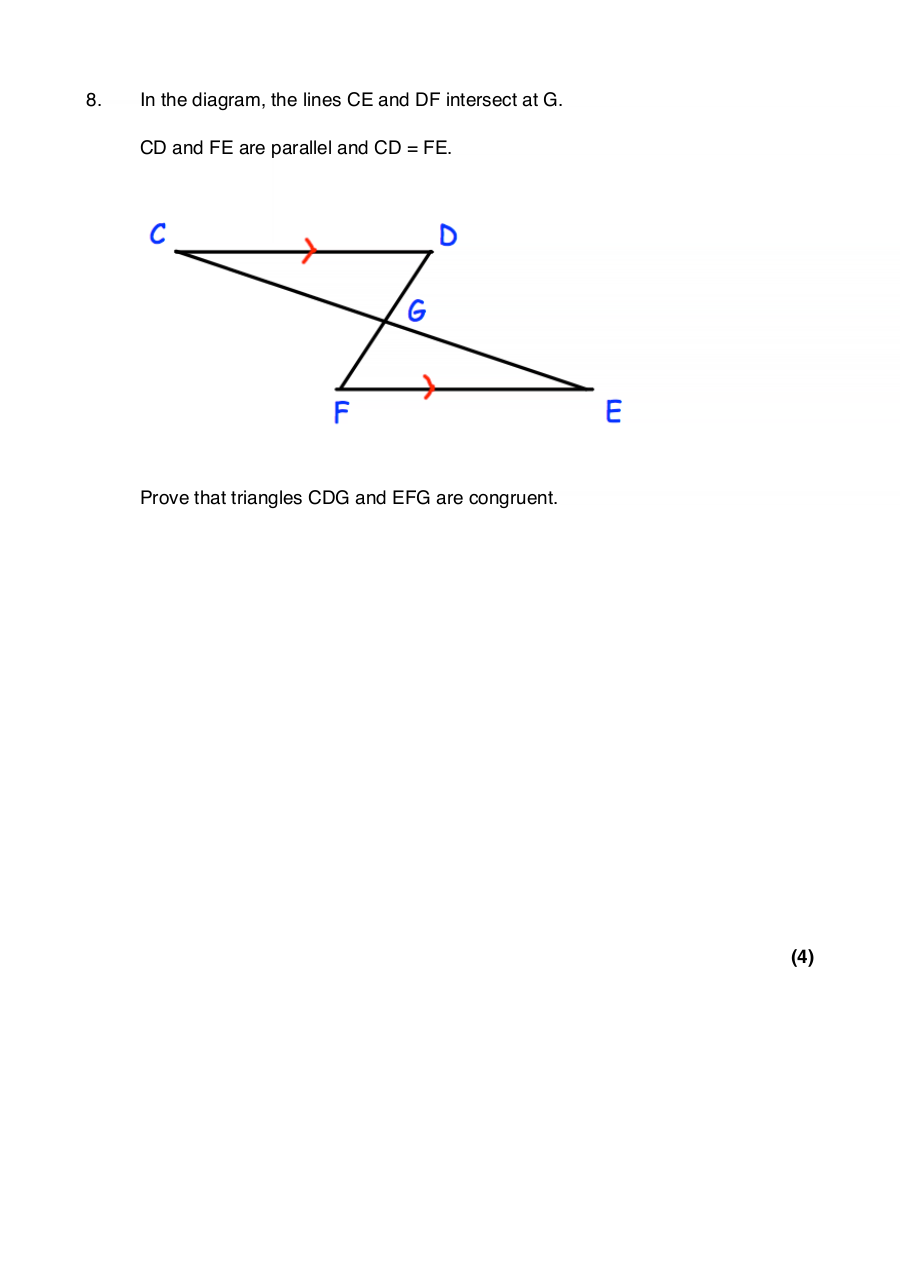
8. In the diagram, the lines CE and DF intersect at G.
CD and FE are parallel and CD = FE.
Prove that triangles CDG and EFG are congruent.
(4)
9.
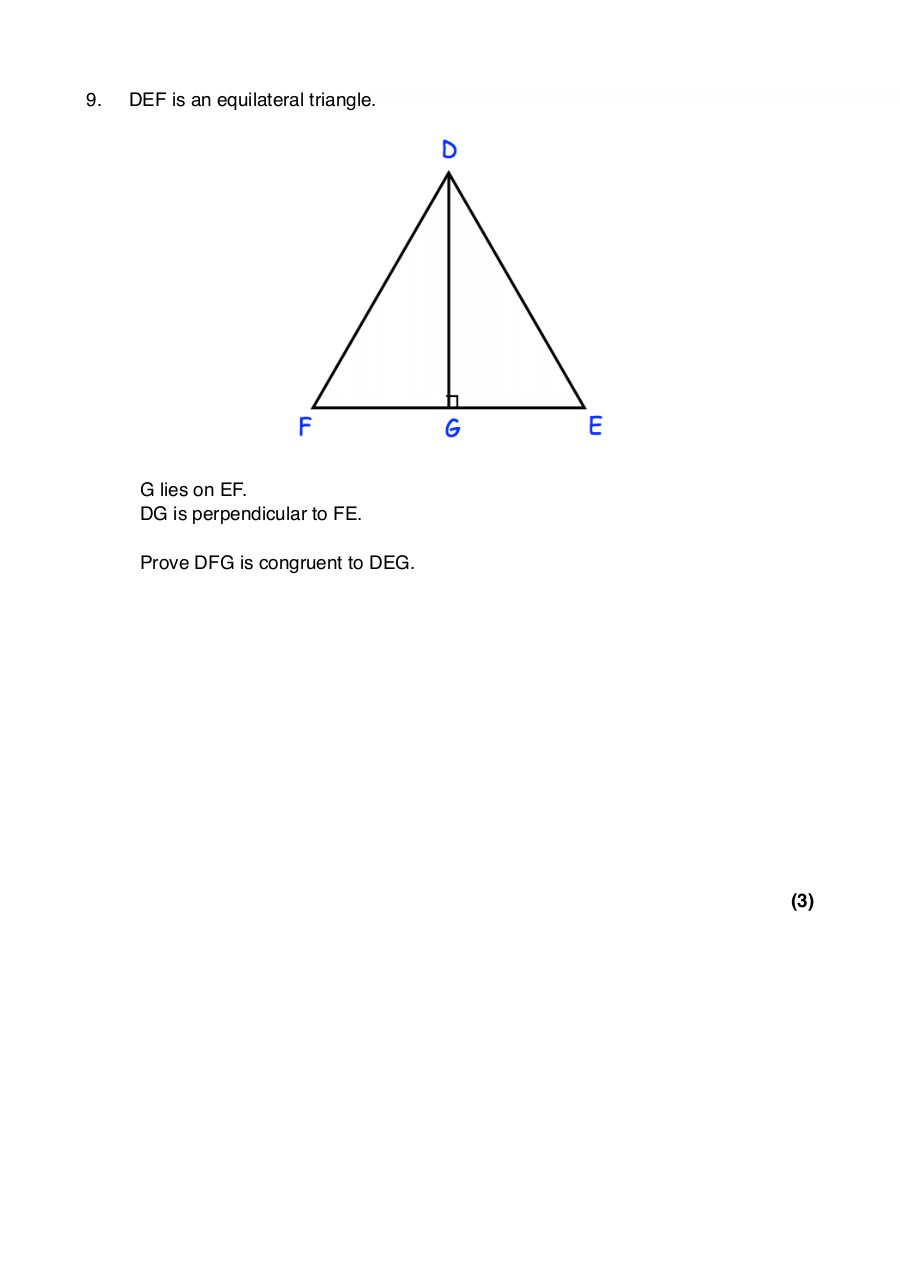
9. DEF is an equilateral triangle.
G lies on EF.
DG is perpendicular to FE.
Prove DFG is congruent to DEG.
(3)
10.
10. ABC is an isosceles triangle in which AC = BC.
D and E are points on BC and AC such that CE = CD.
Prove triangles ACD and BCE are congruent.
(4)
11.
11. ABCD and LMNO are squares.
Angle CBL = x
Prove that triangles ABO and CBL are congruent.
(4)
12.
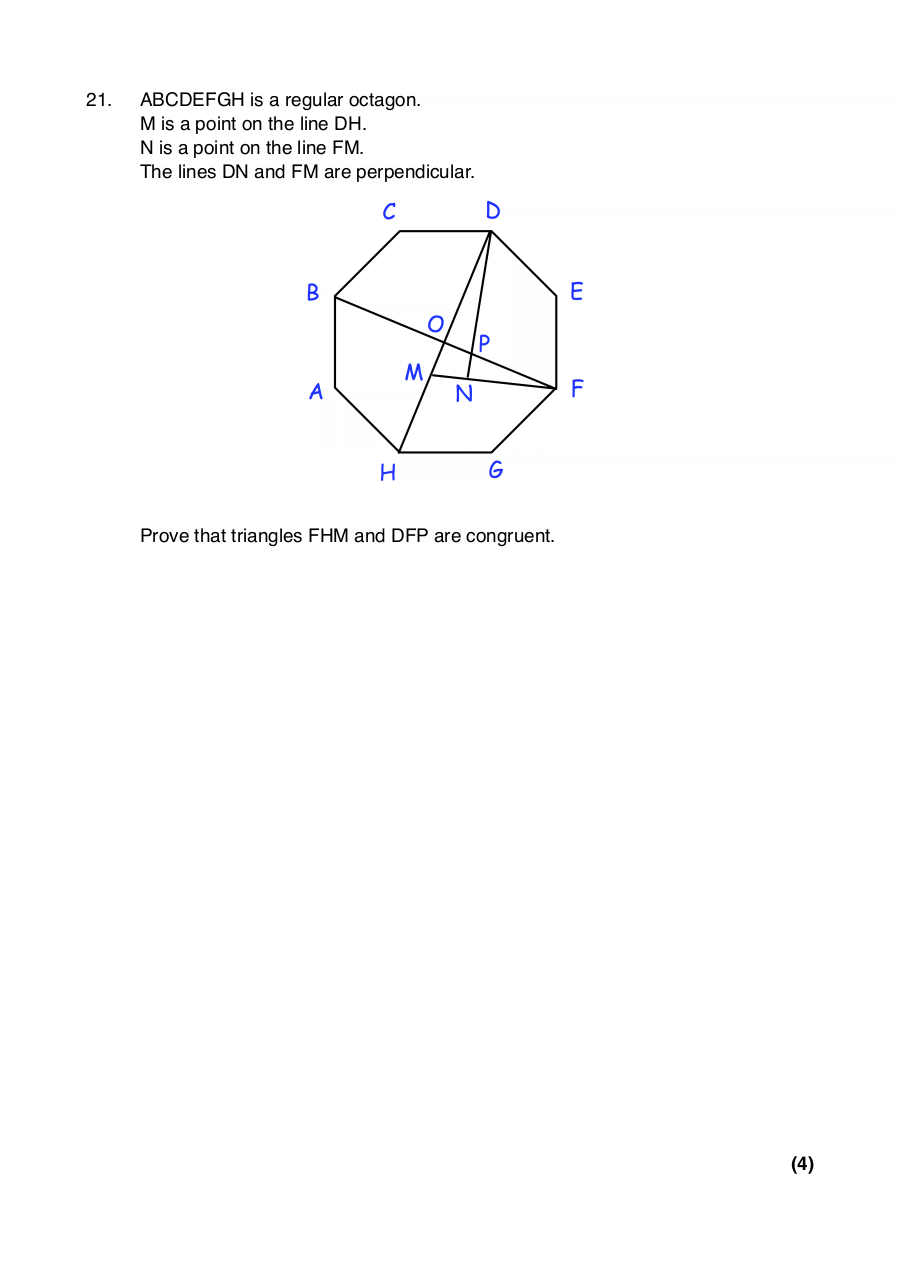
21. ABCDEFGH is a regular octagon.
M is a point on the line DH.
N is a point on the line FM.
The lines DN and FM are perpendicular.
Prove that triangles FHM and DFP are congruent.
(4)