Contributed by:
OCR Foundation NC 2020 NOV
1.
Oxford Cambridge and RSA
F
Thursday 05 November 2020 – Morning
GCSE (9–1) Mathematics
J560/02 Paper 2 (Foundation Tier)
Time allowed: 1 hour 30 minutes
You can use:
* 8 1 8 1 6 1 0 0 7 6 *
• geometrical instruments
• tracing paper
Do not use:
• a calculator
* J 5 6 0 0 2 *
Please write clearly in black ink. Do not write in the barcodes.
Centre number Candidate number
First name(s) �
Last name �
INSTRUCTIONS
• Use black ink. You can use an HB pencil, but only for graphs and diagrams.
• Write your answer to each question in the space provided. You can use extra paper if
you need to, but you must clearly show your candidate number, the centre number and
the question numbers.
• Answer all the questions.
• Where appropriate, your answer should be supported with working. Marks might be
given for using a correct method, even if your answer is wrong.
INFORMATION
• The total mark for this paper is 100.
• The marks for each question are shown in brackets [ ].
• This document has 20 pages.
ADVICE
• Read each question carefully before you start your answer.
© OCR 2020 [601/4606/0] OCR is an exempt Charity
DC (NF/CB) 190041/7 Turn over
2.
2
Answer all the questions.
1 (a) Work out.
(i) -1 + 6
(a)(i) .......................................................... [1]
(ii) 7- - 3
(ii) .......................................................... [1]
(b) Write down two prime numbers between 10 and 20.
(b) ......................... and ......................... [2]
2 (a) (i) Write 350 centimetres in metres.
(a)(i) ....................................................... m [1]
(ii) Write 1.52 litres in millilitres.
(ii) ...................................................... ml [1]
(b) Work out.
5.7 cm + 30 mm.
Give your answer in centimetres.
(b) ..................................................... cm [2]
© OCR 2020
3.
3
3 (a) Complete each statement by writing the missing value in the box.
1 2
(i) = [1]
3 d
1 d
(ii) 1 = [1]
7 7
(b) Work out.
(i) 0.8 ' 2
(b)(i) ......................................................... [1]
(ii) 1.7 # 2
(ii) .......................................................... [1]
4 (a) Write 0.16 as a fraction in its simplest form.
(a) .......................................................... [2]
7
(b) Write as a decimal.
20
(b) .......................................................... [2]
© OCR 2020 Turn over
4.
4
5 (a) Write down the mathematical name of each of these shapes.
(i) A triangle with 3 equal sides.
(a)(i) .............................................. triangle [1]
(ii) A quadrilateral with 4 equal sides and no right angles.
(ii) .......................................................... [1]
(b) Here is a rectangle.
(i) On the diagram, draw the rectangle’s two lines of symmetry. [1]
(ii) The rectangle has rotation symmetry of order 2.
Amaya says
A rectangle is the only quadrilateral that has rotation symmetry of order 2.
Is she correct?
Show how you decide.
..................................................................................................................................... [2]
© OCR 2020
5.
5
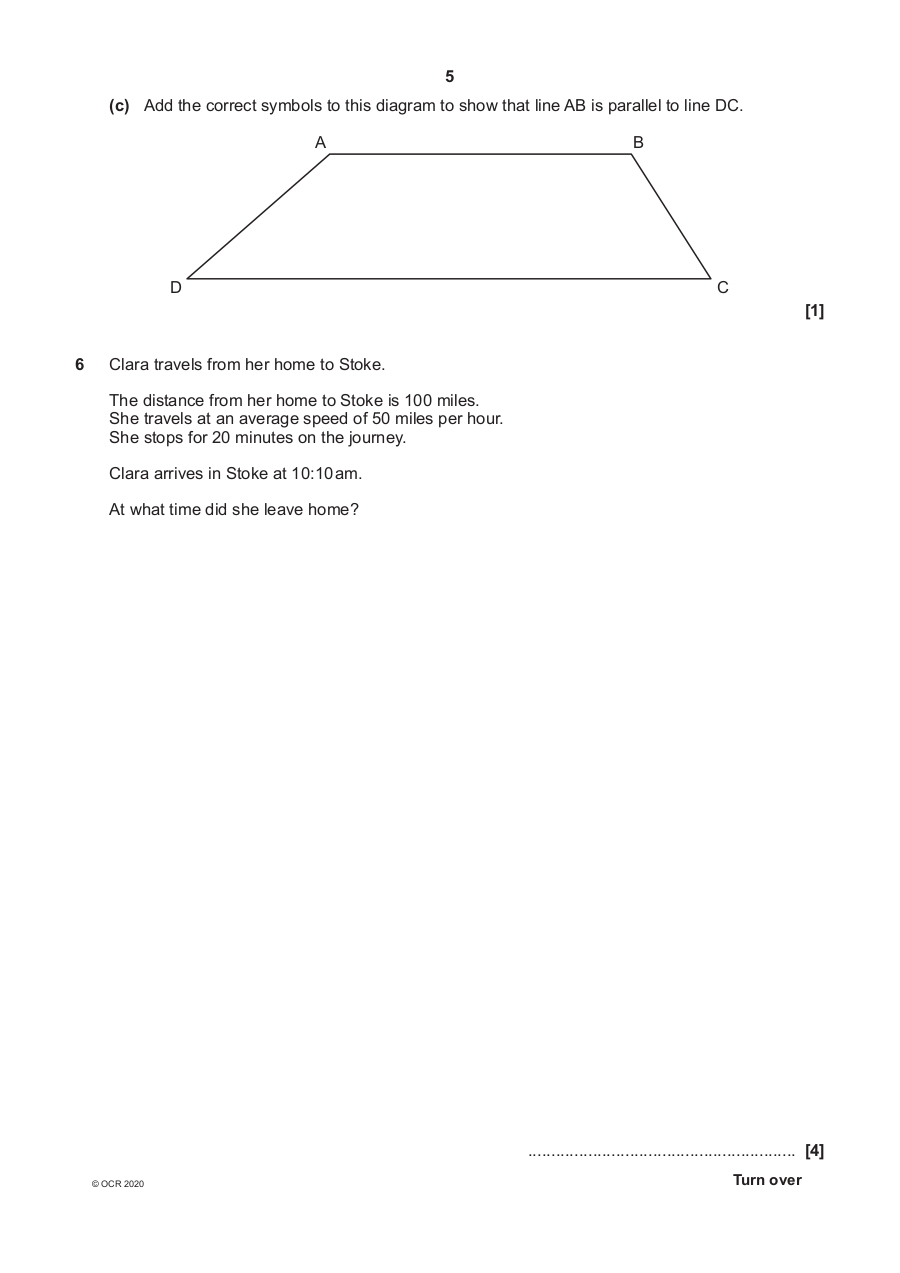
(c) Add the correct symbols to this diagram to show that line AB is parallel to line DC.
A B
D C
[1]
6 Clara travels from her home to Stoke.
The distance from her home to Stoke is 100 miles.
She travels at an average speed of 50 miles per hour.
She stops for 20 minutes on the journey.
Clara arrives in Stoke at 10:10 am.
At what time did she leave home?
.......................................................... [4]
© OCR 2020 Turn over
6.
6
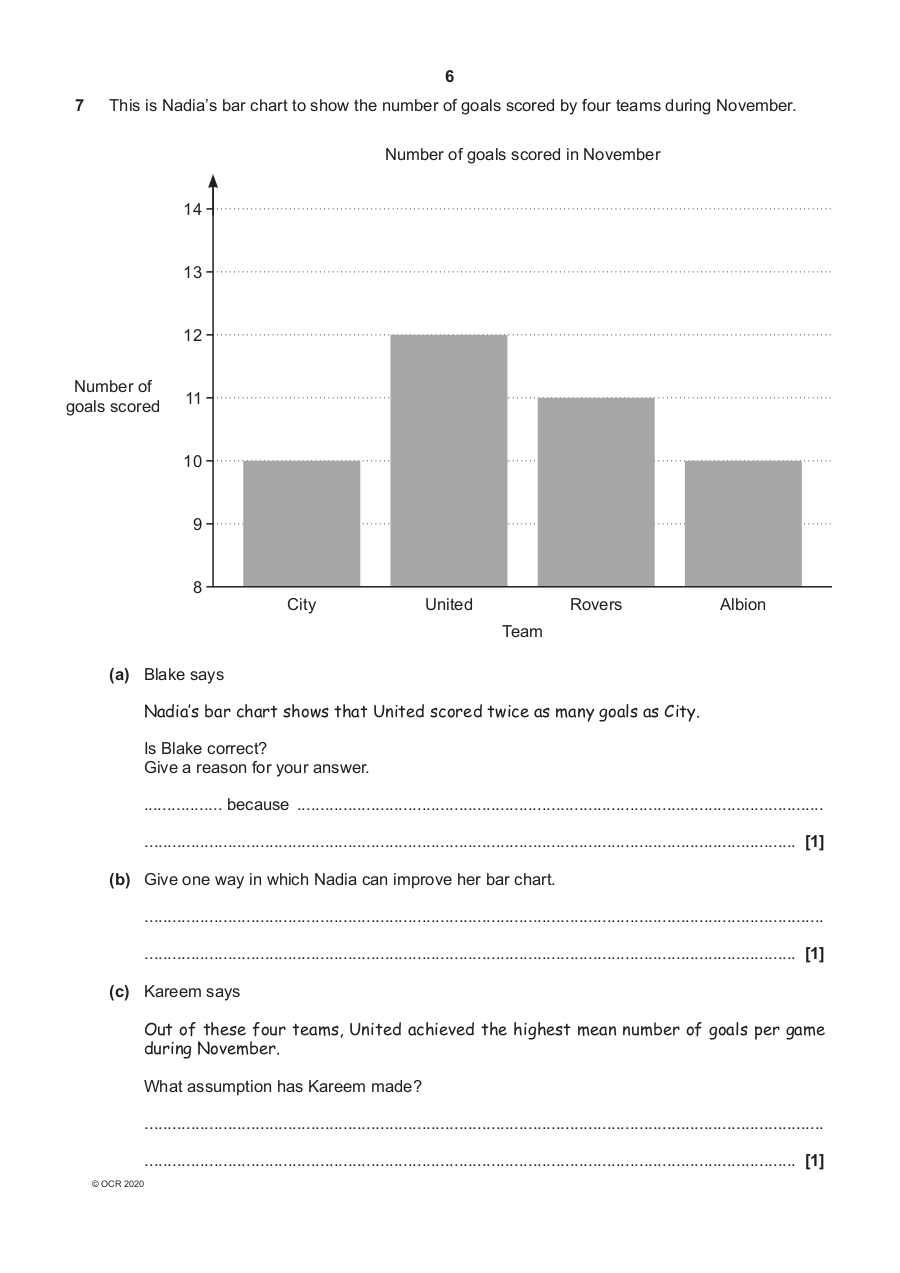
7 This is Nadia’s bar chart to show the number of goals scored by four teams during November.
Number of goals scored in November
14
13
12
Number of
11
goals scored
10
9
8
City United Rovers Albion
Team
(a) Blake says
Nadia’s bar chart shows that United scored twice as many goals as City.
Is Blake correct?
Give a reason for your answer.
................. because ..................................................................................................................
............................................................................................................................................. [1]
(b) Give one way in which Nadia can improve her bar chart.
...................................................................................................................................................
............................................................................................................................................. [1]
(c) Kareem says
Out of these four teams, United achieved the highest mean number of goals per game
during November.
What assumption has Kareem made?
...................................................................................................................................................
............................................................................................................................................. [1]
© OCR 2020
7.
7
8 (a) Write 3 # 3 # 3 # 3 as a power of 3.
(a) .......................................................... [1]
6 -1
(b) Show that the answer to 2 # 4 is a square number.
............................................................................................................................................. [3]
9 Write each of the following ratios in their simplest form.
(a) 12 : 15
(a) ........................... : ............................ [1]
(b) 600 g : 1.8 kg
(b) ........................... : ............................ [3]
10 Simplify.
6
5b
(a)
2
b
(a) .......................................................... [1]
4 3
(b) (x )
(b) .......................................................... [1]
© OCR 2020 Turn over
8.
8
11 Theo invests £500 at a rate of 6% per year simple interest.
(a) Work out the interest he receives in one year.
(a) £ ........................................................ [2]
(b) Work out the value of his investment after 5 years.
(b) £ ........................................................ [2]
12 A jacket has its price reduced by 20% in a sale.
The sale price is £56.
Work out the price of the jacket before the sale.
£ ........................................................ [3]
© OCR 2020
9.
9
13 A bag only contains red, blue, yellow and white counters.
A counter is taken at random from the bag.
The table shows the probability it is red and the probability it is blue.
Colour red blue yellow white
Probability 0.24 0.34
There are twice as many yellow counters as white counters in the bag.
Complete the table. [5]
© OCR 2020 Turn over
10.
10
14 (a) (i) Sketch the graph of x = 3.
Show clearly the value of any intercepts.
y
O x
[2]
2
(ii) Sketch the graph of y = x + 1.
Show clearly the value of any intercepts.
y
x
O
[2]
© OCR 2020
11.
11
1
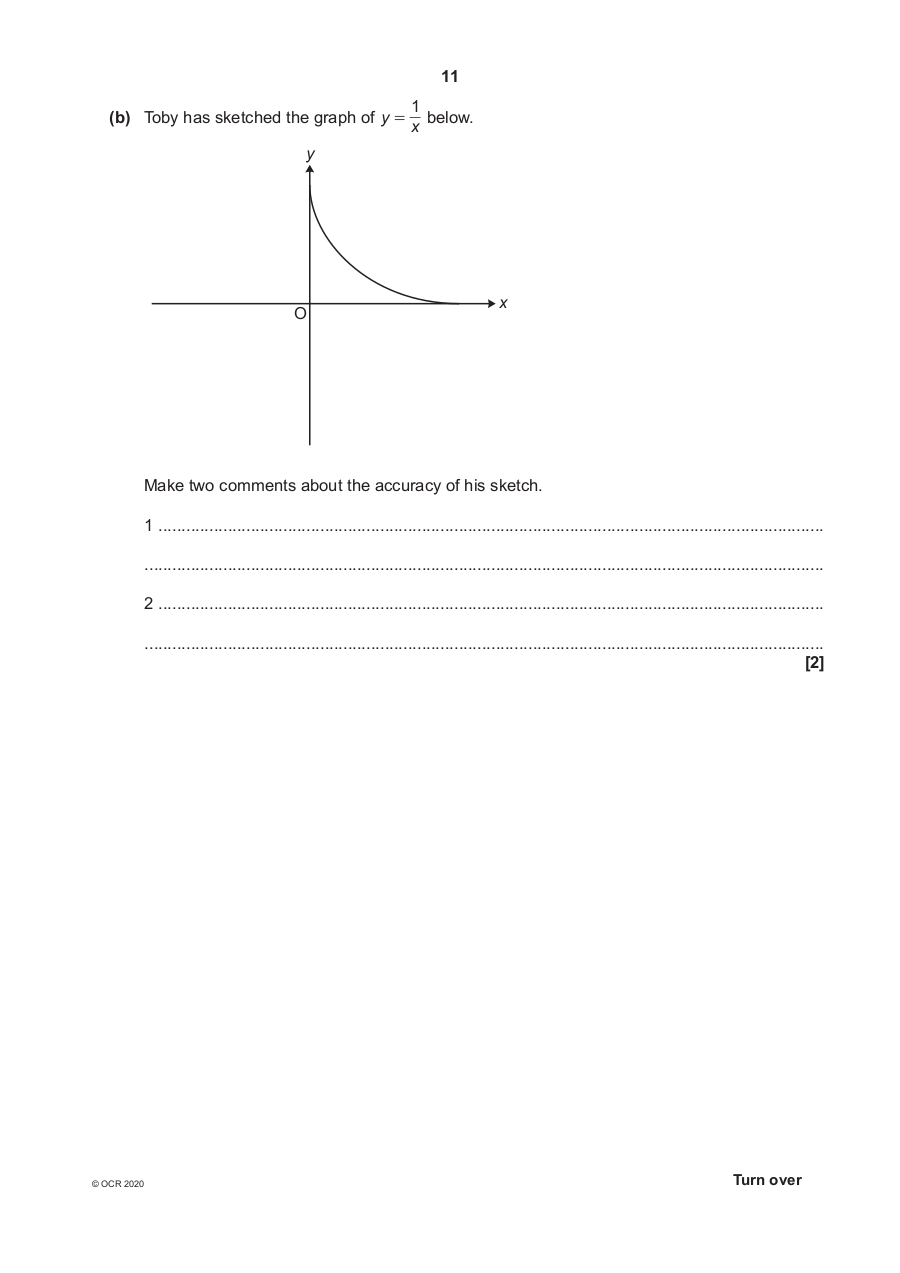
(b) Toby has sketched the graph of y = below.
x
y
x
O
Make two comments about the accuracy of his sketch.
1 ................................................................................................................................................
...................................................................................................................................................
2 ................................................................................................................................................
...................................................................................................................................................
[2]
© OCR 2020 Turn over
12.
12
15 (a) Simplify.
4a - 2b - 2a + 5 b
(a) .......................................................... [2]
(b) (i) Multiply out.
4 (x + 3)
(b)(i) .......................................................... [1]
(ii) Multiply out and simplify.
(x + 5) (x - 2)
(ii) .......................................................... [2]
© OCR 2020
13.
13
16 The diagram shows a square.
(4x – 10) cm Not to scale
(11 – 2x) cm
By setting up and solving an equation, show that the perimeter of the square is numerically equal
to the area of the square.
.................................................................................................................................................... [6]
© OCR 2020 Turn over
14.
14
17 Dora has the following number cards.
2 2 3 5 6
She takes a card at random, replaces the card and then takes a second card.
She adds the numbers on the two cards she has taken and records the total.
(a) Complete the following table to show all of her possible totals.
First card
Total 2 2 3 5 6
2 4 4 5 7 8
2 4 4 5 8
Second
3 5 5 8 9
card
5 7 8 10 11
6 8 8 9 11 12
[1]
(b) Find the probability that her total is
(i) an even number,
(b)(i) .......................................................... [2]
(ii) a multiple of 3 or 4.
(ii) .......................................................... [2]
© OCR 2020
15.
15
18 Charlie and Jasmine share cartons of apple juice.
1
Charlie drinks of a carton every day.
3
2
Jasmine drinks of a carton every day.
5
Any apple juice left in a carton at the end of the day is used the following day.
The cost of a carton is 70p.
Charlie and Jasmine buy just enough cartons to last them for 10 days.
How much do they spend in total for these cartons?
Give your answer in £.
Show your working.
£ ........................................................ [6]
© OCR 2020 Turn over
16.
16
19 A clock chimes every 20 minutes.
A light flashes every 8 minutes.
The clock chimes and the light flashes together at 08:00.
How many times between 08:01 and 12:30 will the clock chime and the light flash together?
Show your working.
.......................................................... [5]
© OCR 2020
17.
17
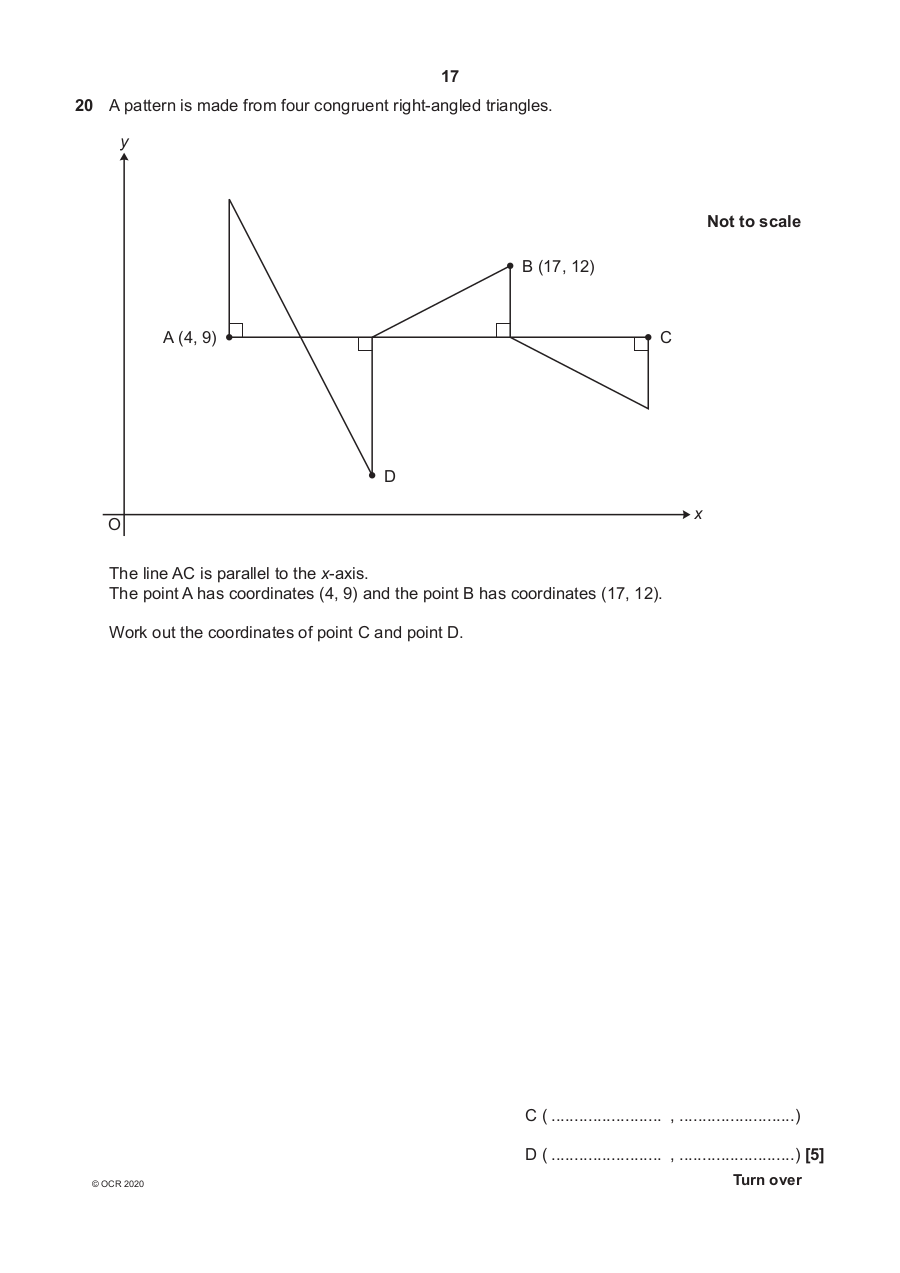
20 A pattern is made from four congruent right-angled triangles.
y
Not to scale
B (17, 12)
A (4, 9) C
D
x
O
The line AC is parallel to the x-axis.
The point A has coordinates (4, 9) and the point B has coordinates (17, 12).
Work out the coordinates of point C and point D.
C ( ........................ , .........................)
D ( ........................ , .........................) [5]
© OCR 2020 Turn over
18.
18
21 Solve the simultaneous equations.
2x + 3y = 10
3x + 5y = 17
x = .....................................................
y = .................................................... [4]
© OCR 2020
19.
19
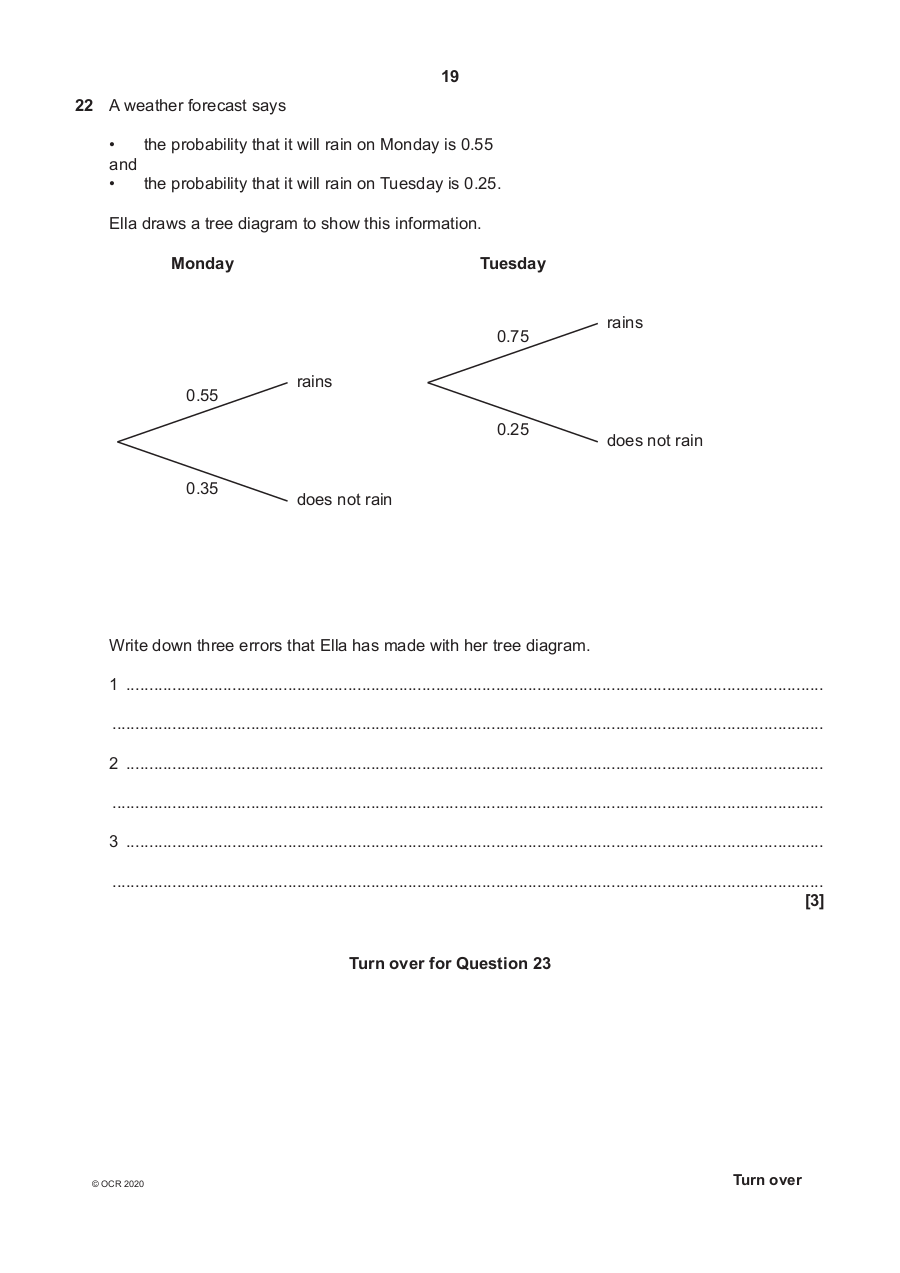
22 A weather forecast says
• the probability that it will rain on Monday is 0.55
and
• the probability that it will rain on Tuesday is 0.25.
Ella draws a tree diagram to show this information.
Monday Tuesday
rains
0.75
rains
0.55
0.25
does not rain
0.35
does not rain
Write down three errors that Ella has made with her tree diagram.
1 .......................................................................................................................................................
..........................................................................................................................................................
2 .......................................................................................................................................................
..........................................................................................................................................................
3 .......................................................................................................................................................
..........................................................................................................................................................
[3]
Turn over for Question 23
© OCR 2020 Turn over
20.
20
23 AOB is a sector of a circle, centre O.
Not to scale
A
120°
O B
r cm
The area of the sector is 8 cm2.
Work out the exact value of the radius, r cm.
r = ............................................... cm [4]
END OF QUESTION PAPER
Oxford Cambridge and RSA
Copyright Information
OCR is committed to seeking permission to reproduce all third-party content that it uses in its assessment materials. OCR has attempted to identify and contact all copyright holders
whose work is used in this paper. To avoid the issue of disclosure of answer-related information to candidates, all copyright acknowledgements are reproduced in the OCR Copyright
Acknowledgements Booklet. This is produced for each series of examinations and is freely available to download from our public website (www.ocr.org.uk) after the live examination series.
If OCR has unwittingly failed to correctly acknowledge or clear any third-party content in this assessment material, OCR will be happy to correct its mistake at the earliest possible
For queries or further information please contact The OCR Copyright Team, The Triangle Building, Shaftesbury Road, Cambridge CB2 8EA.
OCR is part of the Cambridge Assessment Group; Cambridge Assessment is the brand name of University of Cambridge Local Examinations Syndicate (UCLES), which is itself a
department of the University of Cambridge.
© OCR 2020